本文介绍一种估计余弦相似度的算法：simHash
前言
上文介绍了一种估计 Jaccard 相似度的方法 minHash，有些场景要使用余弦相似度，比如文本查重；Jaccard 与余弦相似度在使用场景上有一些区别
| Jaccard 相似度 | 余弦相似度 | |
|---|---|---|
| 特征类型 | 集合 | 数值向量 |
| 数据频率 | 不敏感，只关心是否存在，不关心出现频率 | 敏感，出现次数越多的数据权重越大 |
| 计算 | 交集和并集的个数 | 向量的点积和模长 |
文本相似度用余弦相似度更合适，因为 Jaccard 相似度对于所有词一视同仁，如果两篇文档使用的词相同，出现最多的词不同，说明它们的主题不同，但是 Jaccard 相似度等于 1
余弦相似度更能捕捉到文本的主题，且对文本长度不敏感，比如一篇长文档和一篇短文档谈论同一个主题，如果词出现比例相同，余弦相似度是 1
余弦相似度计算公式 \[ cos(A,B)=\frac{A\cdot B}{\Vert A\Vert\Vert B\Vert} = \frac{\sum_{i=1}^nA_iB_i}{\sqrt{\sum_{i=1}^nA_i^2\sum_{i=1}^nB_i^2}} \] 文档的 One-Hot 向量：0, 1 向量，长度 N，N 为文档库词总数
文档的 IF-IDF 向量：对 One-Hot 向量中的 1 乘以词的 TF-IDF 权重
使用 TF-IDF 向量计算两个文档的余弦相似度时，由于向量维度太高（N 可能百万级别），计算成本太高；下面介绍一种降维的估计余弦相似度的方法 Simhash
SimHash
SimHash 是一种为高维特征向量快速生成"指纹"并估计相似度的算法，将高维、稠密的特征向量降维映射到低维的二进制签名，并保证相似的原向量映射后的签名具有较小的海明距离
核心思想
SimHash 是一种估计余弦相似度的算法，由 Moses Charikar 在他的论文 Similarity Estimation Techniques from Rounding Algorithms 中提出，源于随机超平面投影（Random Hyperplane Projection）的思想
它的重要理论依据为：对于两个向量 u, v，在一个随机超平面下，它们落在同一侧的概率越高，u, v 的余弦相似度越高
在论证这个依据前，先介绍几个基本概念
在 n 维空间中：
任意两个线性无关的向量都可以构成一个二维平面
任意两个向量都夹角范围是 0-180°，夹角弧度 θ 属于 [0, π]
- θ = 0，两向量同向，cosθ = 1
- θ = π/2，两向量正交，cosθ = 0
- θ = π，两向量反向，cosθ = -1
余弦相似度是衡量两个向量的方向一致性
- 余弦相似度 = 1：表示两个向量反向一致
- 余弦相似度 = 0：表示两个向量方向正交
- 余弦相似度 = -1：表示两个向量方向相反
向量 u, v 的点积是 u 向 v 做投影，点积值是投影长度，点积符号可以判断夹角类型
- 点积 > 0，夹角为锐角
- 点积 = 0，夹角为直角
- 点积 < 0，夹角为钝角
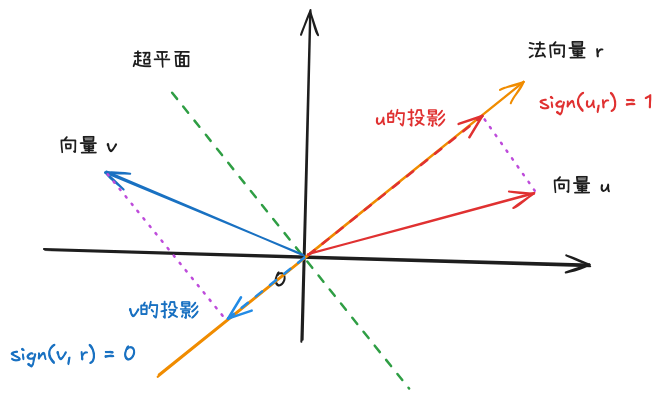
什么是超平面
超平面可以写成 \[ w^Tx+b=0 \] 其中，w 是超平面的法向量，b 是偏置项，x 是空间中任意向量
什么是超平面同侧？
假设超平面法向量指向的一侧为 E，如果向量 u, v 都指向 E 或都不指向 E，则 u, v 同侧，否则 u, v 不同侧
计算方式：u、v 分别与法向量点积，点积符号相同为同侧
符号函数 sign
符号函数用来描述向量在超平面哪一侧；假设超平面 C 的法向量 r，如果向量 u, r 的点积大于等于0，u 在 C 的符号为 1（与 r 同侧），反之符号为 0（与 r 异侧）
对于一个随机超平面，比较两个向量的符号是否一致，可以知道两个向量是否在同侧
\[ sign(u, r)=\left\{ \begin{aligned} &1 &if\ u\cdot r \geq 0\\ &0 &if\ u\cdot r < 0\\ \end{aligned} \right. \]
下面论证 SimHash 的理论依据，首先计算两个向量在随机超平面同侧的概率
先看不同侧的概率：当随机超平面在两个向量之间，切割它们的夹角，则两个向量在超平面的不同侧；因此，超平面切割夹角的概率是：夹角/360*2（超平面是没有方向）
\[
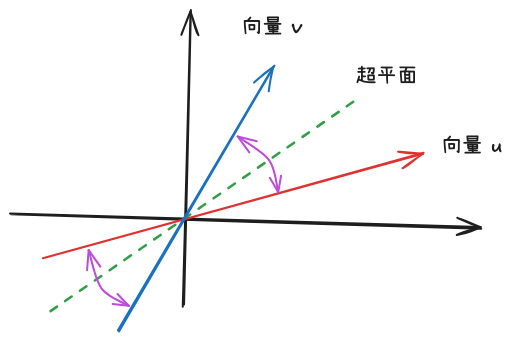P(sign(u, r) \neq sign(v, r)) = \frac{2\theta(u,v)}{2\pi} =
\frac{\theta(u,v)}{\pi}
\] 其中 θ(u, v) 是 u, v 夹角的弧度，u, v 在超平面同侧的概率是
\[
P(sign(u, r) = sign(v, r)) = 1- \frac{\theta(u,v)}{\pi}
\] 对于弧度 θ 有 \[
\theta=arccos(cos(\theta))
\] 两个向量被分到随机超平面同侧的概率可以写成 \[
P(sign(u, r) = sign(v, r)) = 1- \frac{\theta(u,v)}{\pi} =
1-\frac{1}{\pi}arccos(cos(\theta))
\] 其中 cos(θ) 是 u, r 的余弦相似度，由于 arccos(x) 与 x
有严格单调递减关系，所以 P(sign(u, r) = sign(v, r)) 与
cos(θ) 是严格单调递增关系
因此：对于向量 u, v，在一个随机超平面下，它们落在同一侧的概率越高，u, v 的余弦相似度越高
理论到工程
按照上述思路，分成四个步骤；对于文档 A、B：
生成 A、B 的特征向量：分词，计算 A、B 的 TD-IDF 向量 \[ v = [w1, w2,...,w_N] \] N = 词汇表大小（上百万级别）
随机生成若干个超平面：随机生成若干个法向量 ri（N 维随机向量）
做实验：对每个超平面，计算 u, v 与法向量 r 的点积符号：sign(u, r), sign(v, r)
求概率：统计结果，计算 P(sign(u, r) = sign(v, r))
上述过程的计算量非常大，时间复杂度为 O(N*M），M 为超平面个数
优化：文档的 TD-IDF 向量是高维稀疏向量，大量的 0 位对点积结果无影响，可以去掉 0 位得到低维稠密向量
我们将 TD-IDF 向量的 0 位去掉，再与法向量点积，由于每个 TD-IDF 向量非 0 位的原始位置不同，要维护非 0 位在原始向量的下标，再与法向量运算，多了一比额外的空间开销
其实不需要实际生成随机法向量，再去映射位置；只要保证在一次超平面实验中，每个词原始位置在法向量上的值是相同的即可；可以使用哈希函数为每个词生成对应法向量上的值（这与 minHash 使用若干个哈希函数进行随机排列的思想类似）
比如使用 MD5 对词 C 生成一个 64 位 bit 串，一次性对这个词生成了 64 个法向量值，相当于做了 64 次随机超平面实验，第 i 位对应在第 i 个随机超平面法向量上对应位置的值
举个例子：
文档 A = ["水果", "商品", "批发"] 的 TD-IDF 向量 u = [0.4, 0.5, 0.1]
使用哈希函数将 "水果", "商品", "批发" 这三个词映射为长度为 4 的 bit 串
水果 -> [1, 1, 1, 0]
商品 -> [0, 0, 0, 1]
批发 -> [0, 1, 0, 1]
三个 bit 串的第一位，就是第一个随机超平面的法向量 r1 = [1, 0, 0]，第二个随机超平面的法向量 r2 = [1, 0, 1]，第三个随机超平面的法向量 r3 = [1, 0, 0]，第四个随机超平面的法向量 r4 = [0, 1, 1]
文档 A 的 TF-IDF 向量与 r1 的点积为 \[ u \cdot r_1 = 0.4 * 1 + 0.5 * 0 + 0.1 * 0 = 0.4 \] 这样计算出来的点积符号永远是正的，向量都落在超平面法向量一侧了，无法区分
所以将法向量中的 0 视作 -1，即 r1 = [1, -1, -1]，计算如下 \[ u \cdot r_1 = 0.4 * 1 + 0.5 * (-1) + 0.1 * (-1) = -0.2 \]
\[ sign(u, r_1) = sign(-0.2) = 0 \]
对所有超平面依次计算，就得到所有符号
这样完成了第三步【对每个超平面计算 TF-IDF 向量的符号】
下面执行第四步【计算 u, v 符号相等的概率】
假设 u 的符号集合为 [0, 1, 1, 1]，v 的符号集合为 [0, 0, 1, 1]，有 3 位相等，则相等概率为 3/4，用汉明距离可表示为： \[ P = 1 - \frac{HammingDistance(h_u, h_v)}{N} \]
\[ h_u = [sign(u, r_i)], \ i\in[1, N] \]
至此，完成了 simHash 理论到工程的演变，下面看下 simHash 的完整计算步骤
计算步骤
输入一篇文档 Q
分词
使用分词器对文档 Q 进行分词，对停用词清晰，提取出 n 个关键词
例如：["算法", "应用", "数据", "行业"]
hash
使用一个 hash 函数，对每个关键词求 hash 值，转为二进制，取二进制的前 n 位得到每个词在 n 个法向量上对应的值（对应步骤二）
假设 n = 5
算法 = [10110]
应用 = [01001]
数据 = [11001]
行业 = [10011]
加权
计算关键词的 TF-IDF，对关键词的 hash 向量加权，如果 hashi = 1，加权后为权重值，如果是 0，加权后为负的权重值
假设 "算法", "应用", "数据", "行业" 的 TF-IDF 依次是 5, 3, 4, 2 （ TF-IDF 向量 = [5, 3, 4, 2]）
加权后
算法 = [5 -5 5 5 -5]
应用 = [-3 3 -3 -3 3]
数据 = [4 4 -4 -4 4]
行业 = [2 -2 -2 2 2]
合并
合并所有的特征向量
合并后 = [5-3+4+2, -5+3+4-2, 5-3-4-2, 5-3-4+2, -5+3+4+2] = [8, 0, -4, 0, 4]
这里其实与 "水果商品批发" 例子中的计算过程是一样的，只是顺序不同
"水果商品批发" 例子是依次计算特征向量与法向量的点积组合起来，这里是先对特征向量每一位乘以法向量，再把加权后的向量相加
降维
合并后的向量中的每一位，如果大于 0 降维为 1，否则为 0，得到最终的simhash 指纹签名
simHash(Q) = [1, 0, 0, 0, 1]
降维是计算点积符号，加权、合并、降维 对应步骤三
相似度计算
simHash(Q) = [1, 0, 0, 0, 1]，simHash(R) = [1, 1, 0, 1, 1]，汉明距离 = 2，余弦相似度 ≈ 1 - 2/5 = 0.6（对应步骤四）
与 simHash 的比较
| simHash | minHash | |
|---|---|---|
| 核心思想 | 基于随机投影，将高维特征映射到低维签名，期望相似向量的海明距离小 | 基于集合的随机排列，最小哈希值相等的概率等于 Jaccard 相似度 |
| 设计目标 | 估计余弦相似度 | 估计 jaccard 相似度 |
总结
本文介绍了一种估计余弦相似度的方法 simHash， 并对核心思想进行推导，到工程化的演变历程；SimHash 在 Google 检索中扮演着「网络去重过滤器」的关键角色，通过生成局部敏感的指纹，精准地识别并过滤掉大量的重复和近似重复网页