本文讨论的问题:大规模数据的近似最近邻问题(Approximate Nearest Neighbor,ANN)
讨论的范围:由于不同类型的数据处理方法区别较大,本文只讨论可以用集合表示的数据,如文档(词项集合)、基因序列,用 Jaccard 相似度衡量两个集合的相似程度
ANN
近似最近邻,Approximate Nearest Neighbor 是一种在高维空间中寻找与目标点最接近的 K 个点的算法,适合处理大规模、高维度数据,在保证高检索精度的同时显著提高效率,被广泛应用在推荐系统、图像检索、语音识别等场景
为什么需要 ANN
- 维度灾难:在高维空间中,距离计算变得非常复杂
- 海量数据:对于大规模数据,暴力搜索的耗时太长
与 KNN 的区别
- KNN:精确返回最近的 K 个点
- ANN:也返回 K 个,不需要精确,保证一定准确率即可
下面按 One-Hot、minHash、局部敏感性哈希的顺序,看下 ANN 的实现原理
One-Hot
我们知道文档可以转为 One-Hot 编码,然后通过 Jaccard 相似度来衡量两两文档的相似度
比如 文档A = [1, 0 , 0, 1, 0],文档B = [1, 1, 0, 1, 1],A 与 B 的相似度为: \[ Jaccard(A, B) = \frac{A \cap B}{A \cup B} = \frac{2}{4} = 0.5 \] One-Hot 编码在 KNN 的时间复杂度是 O(d * N),d 是 One-Hot 向量的长度(所有词项的个数,可能是百亿级别),N 为文档数量,时间复杂度太高,在大规模数据上是不可行的
按照最近邻计算时间复杂度,忽略 k 个元素的排序时间(原因:每种方法都会有 logk 的时间,为方便比较先忽略)
minHash
minHash 是一个降维方法,可以快速估计两个集合的相似度(文档 = 词项集合)
核心思想
思路:One-Hot 是一个高维稀疏向量,如果能将高维向量映射到低维空间,还保留原空间的相似度,就可以通过低维向量的计算来估计相似度
核心思想:不直接计算原始文档,而是为每个文档生成一个签名,通过比较签名估计文档相似度
定义
minHash 函数(h) 的定义:对于集合 S,在随机排列 t 下,ht(S) 是 S 在排列 t 下拥有最小位置编号的元素
下面通过一个例子演示 minHash 函数
假设全集的词项为 c, d, e, f, g,A、B 的 One-Hot 向量表示如下
词项 文档A 文档B c 1 1 d 0 1 e 0 0 f 1 1 g 0 1 我们将词项重新随机排列:e, g, c, f, d,得到 A、B 新的 One-Hot 向量
词项 文档A 文档B e 0 0 g 0 1 c 1 1 f 1 1 d 0 1 One-Hot 向量中第一个出现 1 位置对应的词项,就是 minHash 在排序 t 下的结果,即 ht(A) = c,ht(B) = g
为什么 minHash 函数可以估计原始文档的相似度呢?要证明的是:在随机排列 t 下,向量 A 与 B 的 minHash 值相等的概率,等于他们的 Jaccard 相似度
证明过程
在排序 t 的情况下,求 h(A) 等于 h(B) 的概率
第一步:只关注并集
minHash 函数只关心文档存在的词项,对于既不在 A 也不在 B 的词项可以完全忽略,只关心 A ∪ B 的词项
第二步:随机排列的第一个词项
对 A ∪ B 中的词项随机排列,A ∪ B 中每个词项都有相同的概率排到首位,首位的词项记为 X
第三步:分析 X 的来源
X 可能来自于三个区域:A ∩ B,A \ B,B \ A
我们关心的是 h(A) = h(B) 的情况,即 A ∩ B
第四步:计算概率
h(A) = h(B) 当且仅当 A ∩ B 中随机排序后首位词项来自于 A ∩ B,这个事件的概率为: \[ P(首位来自A\cap B)=\frac{|A\cap B|}{|A\cup B|} \] 所以 \[ P(h_t(A)=h_t(B)) = \frac{|A\cap B|}{|A\cup B|} = J(A, B) \] 上面证明了一次随机排列下文档签名相等的概率,等于文档的 Jaccard 相似度;但是我们通过一次随机排列,只能观察到是否相等,相等认为 Jaccard = 1,不相等认为 Jaccard = 0,这样误差是很大的
为解决这个问题,可以做 k 次随机排列,每次排列计算 A 与 B 的 minHash 值,这样为每个文档生成了一个 k 维的签名向量: \[ sign(A) = [h_1(A), h_2(A), ..., h_k(A)] \] \[ sign(B) = [h_1(B), h_2(B), ..., h_k(B)] \]
然后估计 Jaccard 相似度为两个签名向量中对应位置相等的比例: \[ E(J(A,B)) = \frac{1}{k}\sum_{i=1}^kI(h_i(A) = h_i(B)) \] \[ I(x, y) = 1, if\ x = y \]
\[ I(x, y) = 0, if\ x \neq y \]
当 k 足够大时,这个估计值会无限接近 Jaccard(A, B)
对全量数据随机排列的成本很大,不需要真正的排列,可以用一个随机性好的哈希函数将数据散列到不同位置来模拟一次随机排列,对文档 A 的每个词项求哈希值,哈希值最小的词项就是 A 的 minHash 值
下面来看下完整步骤
运行步骤
步骤1:选择单个哈希函数 hash(x)
步骤2:生成 k 个哈希函数
通过以下方式生成 k 个哈希函数: \[ hash_i(x) = (a_i * hash(x) + b_i)\ mod\ M, \ i\in[1, k] \] 其中,ai 与 bi 是随机系数(令 k 个哈希函数相互独立),M 是大质数
步骤3:初始化签名向量 \[ sign(A) = [\infty, \infty, ..., \infty] \] \[ sign(B) = [\infty, \infty, ..., \infty] \]
签名向量长度为 k
步骤4:处理文档词项
对文档中每个词项用所有哈希函数计算哈希值,更新签名;假设 A = c, f, e, g,k=3
| 词项 | K1 | K2 | K3 |
|---|---|---|---|
| c | 5 | 10 | 7 |
| f | 2 | 5 | 4 |
| e | 7 | 6 | 9 |
| g | 3 | 8 | 3 |
A 的签名向量 = [2, 5, 3]
同理生成 B 的签名向量 = [2, 3, 3]
步骤5:估计相似度
比较两个签名向量对应位置,计算相等比例
J(A, B) = 2/3 ≈ 0.667
性能分析
下面分析下 单次比较 两个文档相似度的性能,全集词项个数为 d,文档平均词项个数为 m
| 时间复杂度 | 空间复杂度 | |
|---|---|---|
| One-Hot | O(d) | O(d) |
| minHash | O(k * m) | O(k) |
由于 d >> k * m,所以 minHash 要比 One-Hot 的性能高的多
minHash 优化了单次两两比较的性能,将 One-Hot KNN 的 O(d * N) 优化到 O(k * m * N),但 N 依然是一个很大的数;下面讨论如何对 N 优化
局部敏感性哈希
局部敏感性哈希 Locality Sensitive Hashing(LSH)是一种用于高效近似最近邻搜索的哈希技术,通过相似性敏感的哈希函数,将高维空间中相近的数据以高概率映射到同一哈希桶中,从而大幅度降低搜索复杂度
传统哈希:目的是不相似化,用于数据完整性校验和加密,只要相差一个字符,哈希结果也天差地别
敏感性哈希:目的是保留相似性,相似的输入,希望哈希值相同
核心思想
相似的数据有很大概率映射到同一个桶中,不相似的数据很大概率映射到不同的桶中
形象的比喻:在一个图书馆中有数百万本书,想快速找到所有与《哈利波特》相似的书
暴力方法:一本一本地去和《哈利波特》比较
LSH:制定一个规则,把所有作者为 J.K 罗琳、奇幻类的书都放到固定的几个书架上,只需要对这几个书架上的书与《哈利波特》进行比较
这里的「书架」就是上面所说的「桶」
所以 LSH 分为两个阶段:
- 构建索引:预先将全量数据分配到不同桶中,建立数据到桶号的索引
- 查询:根据索引找到所在桶号,在同一个桶内搜索
下面看下具体步骤
运行步骤
构建索引
步骤一:构造签名向量
假设我们有10个文档:D0, ..., D9,用 k=12 的哈希函数,对这 10 个文档通过 minHash 求出签名向量
假设签名向量如下:
sign(D0) = [12, 5, 23, 9, 6, 28, 7, 69, 55, 3, 15, 26]
sign(D1) = [12, 5, 23, 9, 1, 14, 29, 3, 10, 8, 21, 53]
...
sign(D9) = [90, 11, 46, 32, 7, 4, 25, 88, 3, 21, 49, 36]
步骤二:签名切分
将 k 维的签名向量切分为 n 个 r 维的波段(band),k = n * r
假设 r = 4,将签名向量分成 3 个 band,每个 band 包含 4 个签名
sign(D0) = [12, 5, 23, 9, 6, 28, 7, 69, 55, 3, 15, 26]
sign(D1) = [12, 5, 23, 9, 1, 14, 29, 3, 10, 8, 21, 53]
...
sign(D9) = [90, 11, 46, 32, 7, 4, 25, 88, 3, 21, 49, 36]
步骤三:对 band 求桶号
- 对第 i 个 band,使用一个复合哈希函数 gi 来处理这个 band 的 r 个 minHash 值
- gi(band) = Hash(minHash_1, ..., minHash_r),可以将 r 个 minHash 值拼成一个字符串,然后求哈希值,作为对应的桶号
比如:
D0: [bucket1, bucket4, bucket64]
D1: [bucket1, bucket35, bucket236]
...
D9: [bucket35, bucket356, bucket893]
步骤四:构建哈希表
- 对第 i 位 band,将桶号相同的文档放入对应的桶中
- 重复构建:对 n 个 band 分别构建 n 张哈希表(不同位置的 band 不可比较)
例如:
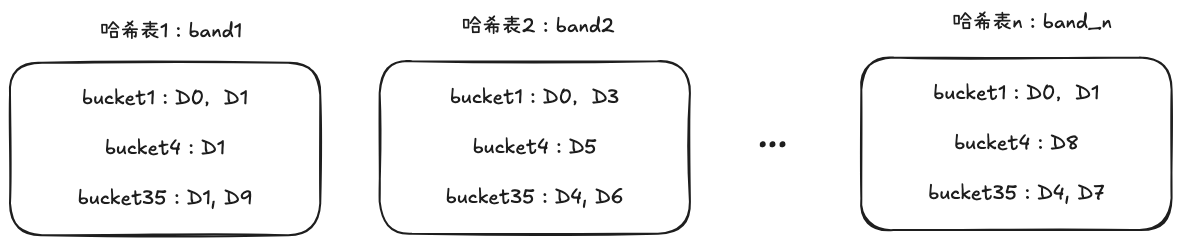
这样就建立了 n 张桶与文档的关系表
查询
桶内比较相似度
输入目标文档 T,最相似的文档个数 K
- 遍历 n 张哈希表,根据索引找到文档 T 所在的桶(若干个)
- 对这些桶中的文档依次与 T 计算 minHash 相似度
- 返回相似度最大的 K 个文档
这个过程避免了全量数据的遍历,极大提高了效率
参数选择
LSH 涉及的参数:
r:band 的维度
n:一个签名向量中 band 的数量,也是哈希表的个数
k:签名向量的长度(minHash 哈希函数的个数)
k = r * n
参数 r 的选择对结果的影响很大,先看两个极端情况:
情况一:r = 1,n = k
band 长度为 1,只要有一个位置的 minHash 值相同就会落到同一个桶里,这样做的结果是:
- 桶多,桶内元素多
- 索引空间大,计算量大
- 召回率高
情况二:r = k,n = 1
band 长度为 k,需要所有位置的 minHash 都相同才落到同一个桶里,这样做的结果是:
- 桶少,桶内元素少
- 索引空间小,计算量小
- 召回率低
在 k 不变的情况下,r 越小召回率越高,存储、计算量越大
参数的影响:
| 参数调整 | 召回率 | 准确率 | 效率 | 原因 |
|---|---|---|---|---|
| 增加 k | 降低 | 提高 | 降低 | 签名更长、更精确,但计算和比较成本更高。更严格的匹配条件降低了召回率(n 不变) |
| 增加 r | 提高 | 降低 | 降低 | 每个 band 的条件更苛刻,只有高度相似的对才能碰撞。误报大大减少,候选集更小,但漏报增加 |
| 增加 n | 降低 | 提高 | 提高 | 更多「抽奖」机会,相似对更可能被捕获,但也不相似的对也更易混入(误报)。需要更多的哈希表(n张),内存增加 |
我们当然希望召回率越高越好,这样就不会有漏网之鱼,但是高召回率意味着更大的存储空间和计算量,应该如何取舍呢?可以通过计算召回率来估计参数
召回率计算推导
假设文档 A, B 的 Jaccard 相似度 = minHash(A, B) = sim,哈希签名拆分为 k = n * r,由于哈希签名中每个位置是相互独立的,所以每个位置相等的概率都是 sim,则:
一个 band 相等的概率 = simr
n 个 band 都不相等的概率 = (1-simr)n
至少有一个 band 相等的概率 = 1 - (1-simr)n
说明对于相似度 sim 的两个文档,通过 LSH 计算,有 1 - (1-simr)n 的概率会被分到一个桶内(在一个桶内就会被搜索,即召回)
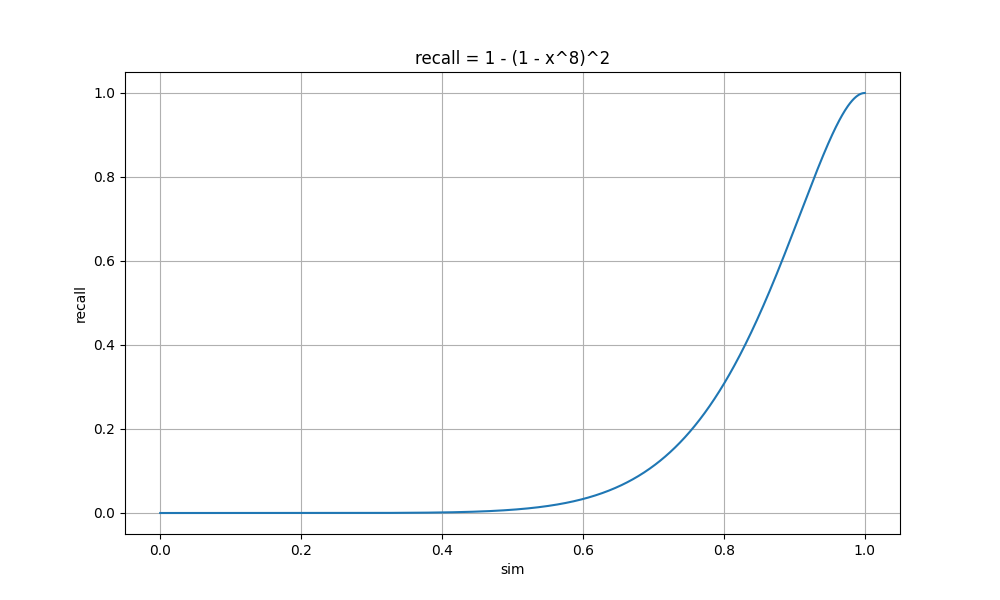
也就是说,LSH 算法在参数 r, n 下的召回率为: \[ recall = 1 - (1-sim^r)^n, \ sim\in [0,1] \] 以 k = 16,画出不同 r 值的 recall 曲线:
| 参数 | 召回率 | |
|---|---|---|
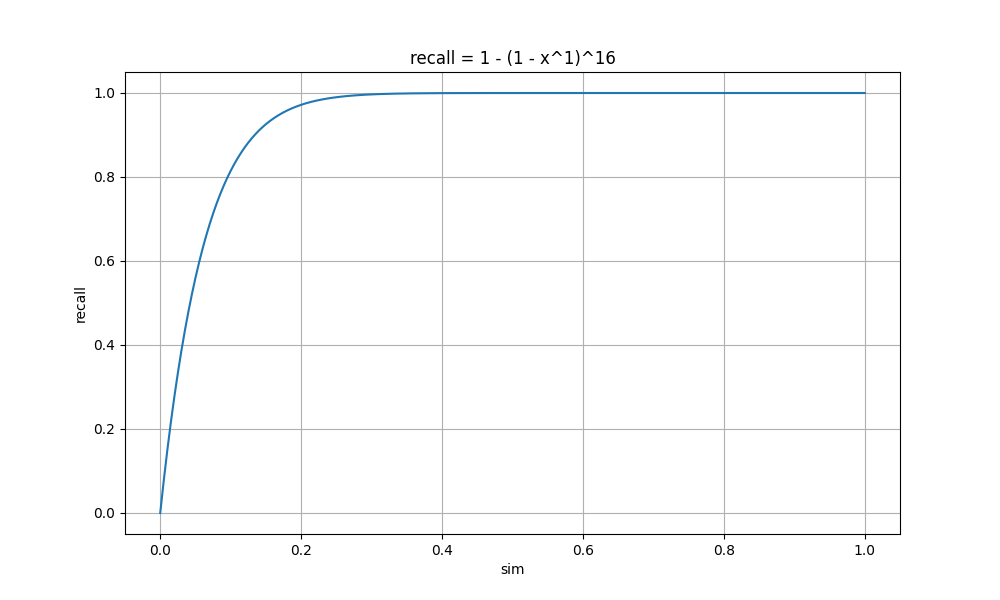
| r = 1 n = 16 |
sim= 0 recall= 0 sim= 0.2 recall= 0.97 sim= 0.4 recall= 1.0 sim= 0.6 recall= 1.0 sim= 0.8 recall= 1.0 sim= 1 recall= 1 |
 |
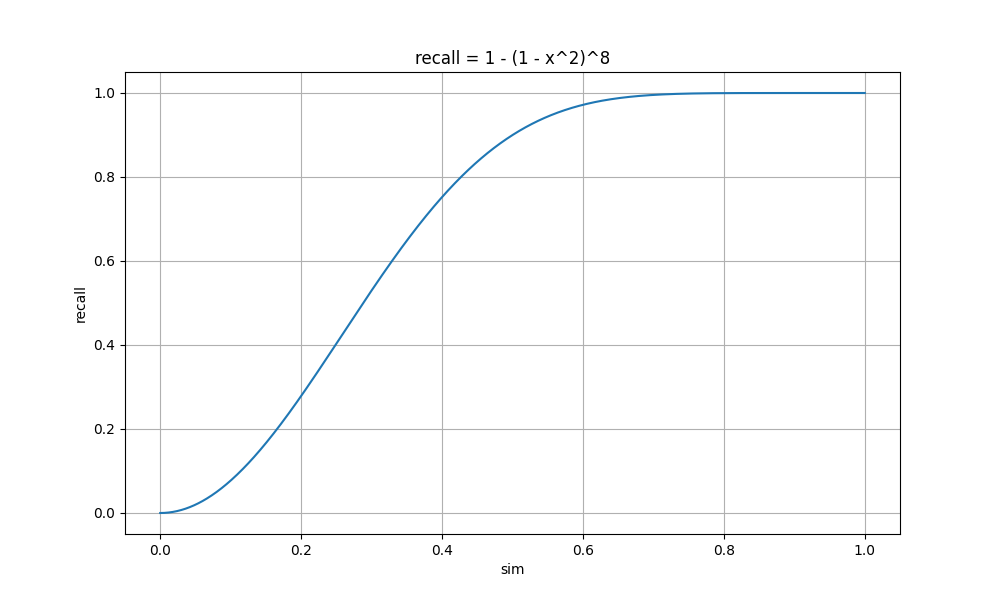
| r = 2 n = 8 |
sim= 0 recall= 0 sim= 0.2 recall= 0.28 sim= 0.4 recall= 0.75 sim= 0.6 recall= 0.97 sim= 0.8 recall= 1.0 sim= 1 recall= 1 |
 |
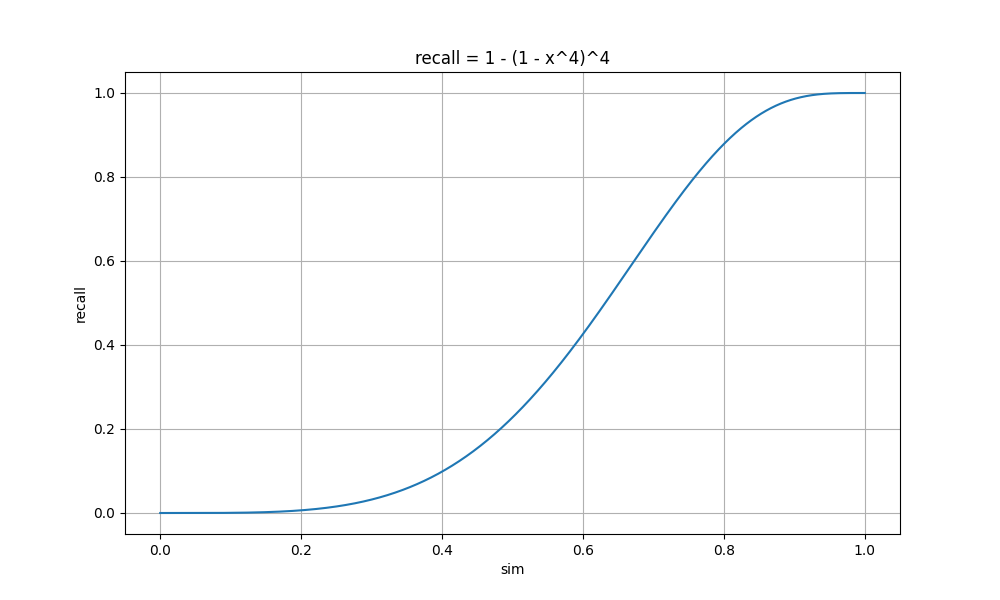
| r = 4 n = 4 |
sim= 0 recall= 0 sim= 0.2 recall= 0.01 sim= 0.4 recall= 0.1 sim= 0.6 recall= 0.43 sim= 0.8 recall= 0.88 sim= 1 recall= 1 |
 |
| r = 8 n = 2 |
sim= 0 recall= 0 sim= 0.2 recall= 0.0 sim= 0.4 recall= 0.0 sim= 0.6 recall= 0.03 sim= 0.8 recall= 0.31 sim= 1 recall= 1 |
 |
| r = 16 n = 1 |
sim= 0 recall= 0 sim= 0.2 recall= 0.0 sim= 0.4 recall= 0.0 sim= 0.6 recall= 0.0 sim= 0.8 recall= 0.03 sim= 1 recall= 1 |
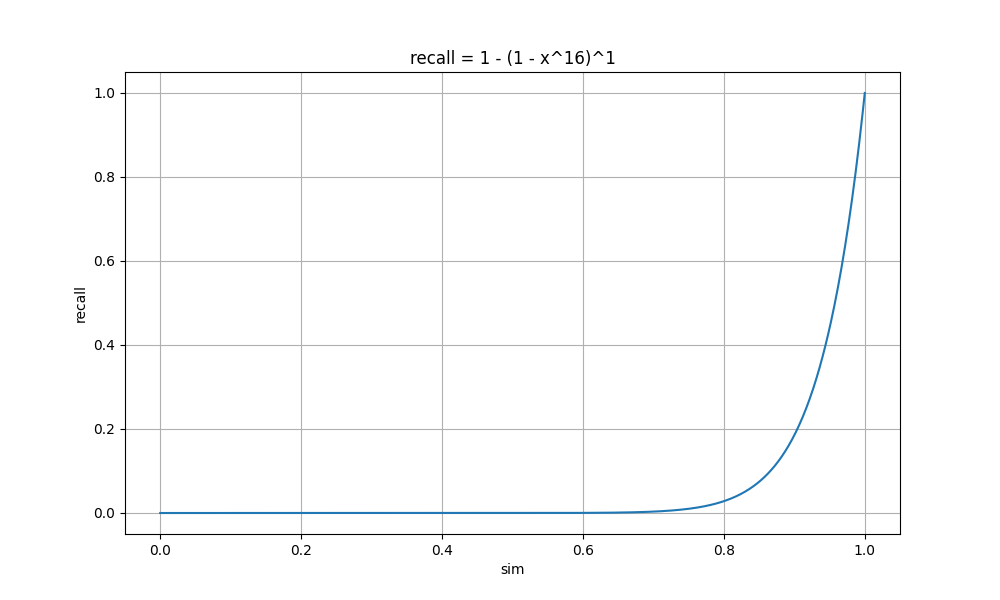 |
可以看到 r 值越小,曲线上升越快,这时较小相似度的文档也会被召回,整体的召回率高,计算量大;
随着 r 值增大,曲线上升变缓,直到某个点开始突增,这时较小相似度的文档召回率几乎为0,相似度大的文档召回率高
下面来看下确定参数的具体步骤:
步骤一:定义业务目标
- 根据应用场景,确定相似度阈值 t:是找到几乎重复(t > 0.9)还是比较相关(t > 0.6)即可
- 可接受的错误率:能接受多少漏报和误报
- 资源限制:预期的计算耗时
步骤二:初步估计
根据公式 P(sim) = 1 - (1-simr)n,预测两个相似度为 sim 的文档称为候选对的概率
假设相似度阈值 t = 0.7,希望 P 曲线在 t 处最陡,相似度高于 t 的文档高概率称为候选对,低于 t 的文档低概率称为候选队,一个经验法是让 r 和 n 满足 \[ t ≈ (1/n)^{(1/r)} \]
- 尝试1:r=5,n=20
- P(0.7) = 1 - (1-0.75)20 ≈ 0.97
- P(0.6) = 1 - (1-0.65)20 ≈ 0.80(0.6 的召回率也比较高,不太好)
- 尝试2:r=6, n=25
- P(0.7) ≈ 0.94
- P(0.6) ≈ 0.70
以此类推找到合适的切割点
步骤三:对测试集做实验
做实验得到实际召回率、准确率、运行时间,再进行微调
性能分析
索引构建阶段
计算 minHash 签名
时间复杂度 O(N * k * m),N:数据总量,k:minHash 签名长度,m:文档平均词数
空间复杂度:O(N * k)
构建 n 张 LSH 哈希表
时间复杂度 O(n * N)
空间复杂度O(n * L)
构建索引的总时间复杂度:O(N * (k * m + n)),空间复杂度:O(N * k + n * L)
查询阶段
分析一次最近邻查询的复杂度
- 计算查询点的 minHash 签名:O(k * m)
- 查找候选集:O(n + C),C 为候选集内数据个数
- 对候选集依次与目标点比较:O(C * m)
查询总时间复杂度:O(k * m + n + C + C * m)
候选集大小 C 取决于 LSH 的调参情况
最坏情况:所有数据都哈希到同一个桶里,此时 C = N,查询复杂度退化为线性扫描 O(N * m) ,在参数设置合理的情况下几乎不会发生
正常情况:C 远小于 N,经过精心调参,可以使 C 达到 logN 甚至 N0.1
比较下 One-hot,minHash 和 LSH 在 KNN/ANN 的复杂度
| 时间复杂度 | 空间复杂度 | |
|---|---|---|
| One-Hot(KNN) | O(d * N) | O(d * N) |
| minHash(ANN) | O(k * m * N) | O(k * N) |
| LSH(ANN) | O(k * m + n + C + C * m) | O(N * k + n * L) |
总结
文本介绍了高维数据、大规模数据的近似最近邻搜索(ANN)方法:minHash 与 局部敏感性哈希,将高维空间中相近的数据点以高概率映射到同一哈希桶中,牺牲了少量精度,极大提高了搜索效率,在大模型数据清洗、推荐系统、查重检测等场景有重要应用