Jiaming Zhang's Blog
0%

K 近邻问题 KNN

发表于 分类于

RAG 在检索时，会在向量数据库中找出与查询向量 P 最相近的 k 个文档向量，如何从海量向量中找出与 P 最相近 k 个向量呢，这是一个 K 近邻问题（ K-Nearest Neighbors，KNN）

本文介绍下问题 KNN 的两种方法

KNN 暴力的方法，可以计算查询点与数据集中每个点的距离，然后全部放入大顶堆中，返回 k 个点，时间复杂度是 O(d * nlogn)，n 是节点个数，d 是维度，当 n 很大时，这种方法会非常耗时

下面介绍两种不需要遍历所有数据的方法

KD-Tree

K-Dimensional Tree，是一种用于组织 k 维空间数据的数据结构，主要用于范围搜索和最近邻搜索

核心思想

递归地对 k 维空间进行划分，将空间划分为若干个小区域

数据结构

二叉树，每个节点保存一个数据和划分维度

构建过程

开始时的 KD-Tree 是空树，递归地向 KD-Tree 上添加子节点，包含以下步骤：

  1. 选择划分维度（split_dim）：当前节点应该基于哪个维度划分，常用有两种方法：

    1. 循环选择：从根节点（深度为0）开始，第 depth 层的节点使用第 (depth % k) 维度来划分，k 为总维度数

      优点：实现简单，计算开销小

      缺点：如果数据在某个维度上方差很小，轮流划分可能不会产生最有效的分割

    2. 最大方差法：在每个节点，计算当前数据集（分配到该节点为根节点子树的数据）在所有 k 个维度上的方差，选择方差最大的维度划分

      思路：方差越大，说明数据越分散，更有效的划分数据集

      优点：通常来说可以生成搜索性能更好的树

      缺点：构建过程计算开销大

  2. 选择划分值（split_value）：在选定的维度下，用什么值来划分，希望划分后两边数据量相差不大，否则会不平衡，最常用的是用中位数

  3. 创建节点：在 KD-Tree 上新建节点，节点的值是 split_value 所在的数据

  4. 划分：根据split_dim 和 split_value，将数据划分为左右两个子集

  5. 向下递归：递归构建左右子树

左子树的数据在 split_dim 上的值一定小于 split_value，右子树的数据在 split_dim 上的值一定大于等于 split_value

举例说明：k=3, n = 6

数据集：A(1, 2, 3), B(4, 5, 6), C(7, 8 ,9), D(10, 11, 12), E(13, 14, 15), F(16, 17, 18)

构建过程：

  1. depth = 0
    1. 选择维度：0 % 3 = 0
    2. 当前数据集：A, B, C, D, E, F
    3. 选择划分值：第 0 维数据=[1, 4, 7, 10, 13, 16]，划分值取中位数 7
    4. 创建节点：划分值对应数据 C(7, 8 ,9) 作为根节点
    5. 划分子树：
      1. 左子树（第 0 维 < 7）：A(1, 2, 3), B(4, 5, 6)
      2. 右子树（第 0 维 >= 7）：D(10, 11, 12), E(13, 14, 15), F(16, 17, 18)
  2. depth = 1 左子树
    1. 选择维度：1 % 3 = 1
    2. 当前数据集：A, B
    3. 选择划分值：第 1 维数据=[2, 5]，划分值取中位数 2
    4. 创建节点：划分值对应数据 A(1, 2, 3) 创建节点
    5. 划分子树：
      1. 左子树：空
      2. 右子树：B(4, 5, 6)
  3. depth = 1 右子树
    1. 选择维度：1 % 3 = 1
    2. 当前数据集：D, E, F
    3. 选择划分值：第 1 维数据=[11, 14, 17]，划分值取中位数 14
    4. 创建节点：划分值对应数据 E(13, 14, 15) 创建节点
    5. 划分子树：
      1. 左子树：D(10, 11, 12)
      2. 右子树：F(16, 17, 18)

当前节点包含的数据只有1个时，递归结束，该节点作为叶子节点

最终的 KD-Tree 为

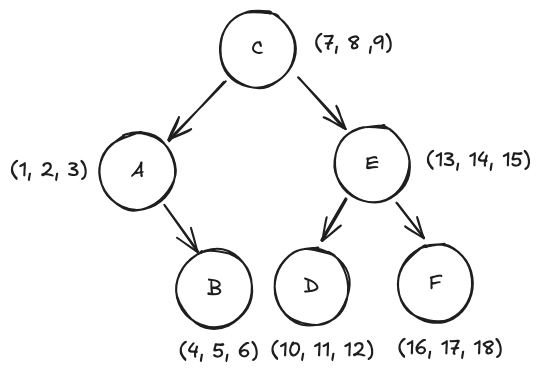
dk-tree

搜索过程

下面介绍 DK-Tree 的两个常见的应用场景：范围搜索 和 KNN

DK-Tree 的范围搜索

假设搜索范围为 [min0, max0] * [min1, max1] * ... * [mink, maxk]

搜索过程从根节点开始，递归进行以下判断：

  1. 如果当前节点 P 在范围内，将 P 加入到结果集中
  2. 决定递归搜索哪个子树：
    1. 确定 P 的划分维度 d，P 在 d 维度的值为 x
    2. 如果 x <= minp，说明左子树所有节点的 d 维度值都小于 minp，左子树可以剪枝，否则遍历左子树
    3. 如果 x > maxp，说明右子树所有节点的 d 维度值都大于 maxp，右子树可以剪枝，否则遍历右子树
  3. 递归终止条件：当前节点为空

DK-Tree 的 KNN 搜索

暴力的 knn 是遍历整颗树，计算每个节点与目标点 P 的距离，找到距离最小的 n 个节点。可以利用 KD-Tree 的特性来剪枝提高遍历效率

假设当前已经遍历了 n 个节点，最大距离是 dmax，如果子树中所有节点到 P 的最小距离大于 dmax，则可以直接跳过该子树；但是最小距离还是要遍历整颗子树才能得到，转为计算 P 到子树的超平面距离的方式

子树的超平面：由子树跟节点的 split_dim 和 split_value 定义的无限平面

在 DK-Tree 中，每个节点可以看做对当前数据集在 split_dim 维度用 split_value 分割成两部分，split_dim 与 split_value 就构成了一个超平面，左子树的数据都在超平面的一侧，右子树的数据都在超平面的另一侧

设 P 到超平面的距离为 dist

核心思想：以 P 为中心，半径 dmax 为半径的超圆面，如果超圆面与超平面没有交集，则对超平面另一侧剪枝，具体为：

  • 如果 dmax < dist，另一侧整个空间都不存在更近的点，可以剪枝
  • 如果 dmax >= dist，另一侧可能存在更近的点，不可剪枝
超平面

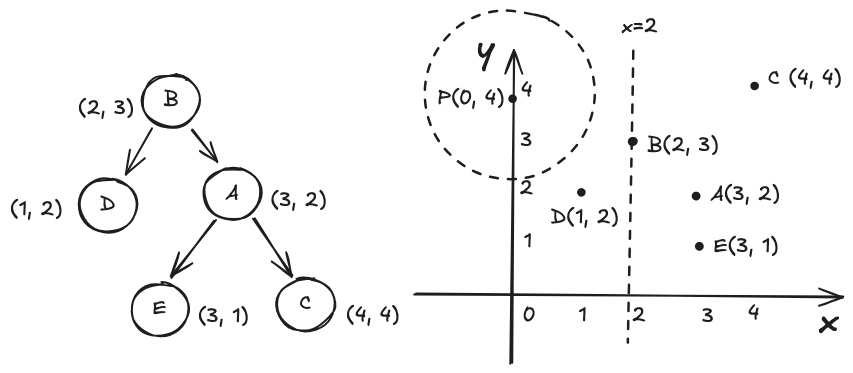
我们将整个过程分为几个阶段，假设 K=1（最近邻），可以轻松的推广到 K > 1

阶段一：确定初始节点

找到目标点 P 较近的点，得到较小的初始距离作为比较基准，有利于剪枝

  1. 从根节点开始，比较 P[split_dim] 与 split_value 大小
  2. 如果 P[split_dim] < node.split_value，进入左子树，否则进入右子树；
  3. 直到叶子节点 D，计算 min_dist = dist(P, D)

阶段二：回溯父节点

假设 N 的左子节点是 P，右子节点是 R

  1. 回溯到父节点 N，计算 dist(P, N)，如果 dist(P, N) < min_dist，则 N 为最近邻，更新 min_dist
  2. 计算 P 到 N 的划分超平面的距离 d，如果 d > min_dist，另一侧不可能存在更近邻的点，跳过整个另一侧子树；如果 d <= min_dist，可能存在更近的点，继续检索

阶段三：检索另一侧子树

另一侧子树的根节点为 R

  1. 从 R 开始，递归执行阶段一、二、三
  2. 递归结束条件：回溯到 R
  3. 递归调用完成后，会带着子树中找到的最佳结果返回

阶段四：继续向上回溯

完成了对子树 N 所有数据的检查后，继续向上回溯 N 的父节点，重复上述阶段，直到回溯到整个树的根节点

在最近邻（K=1）问题中，超球面半径是 min_dist，当 K > 1 时，替换成大顶堆堆顶值即可

优缺点

优点：

  1. 低维空间查询高效：对于低维数据（通常 k < 10~20），性能远高于暴力线性扫描，时间复杂度可接近O(logn)
  2. 实现简单
  3. 内存开销小
  4. 适用于精确查询

缺点：

  1. 维度灾难：当数据维度 k 较高时，KD-Tree 的性能会急剧下降，甚至退化为近似线性扫描（原因：高维度空间，以查询点为圆心的超球面更大概率与划分超平面相交，剪枝效率大大降低）
  2. 对数据分布敏感：当某个维度的数据分布不均，可能导致分割后两边数据量差异很大，会出现很不平衡的树
  3. 不适合动态数据集：如果数据要频繁变更，维护树的平衡性的代价会非常高昂
  4. 不适合非欧式空间：KD-Tree 严重依赖于欧几里得空间的坐标轴，对于其他距离度量（如余弦距离）无法适用

为了解决 KD-Tree 在高维空间下效率问题，下面介绍一下 Ball-Tree

Ball-Tree

Ball-Tree 是一种专门解决 KD-Tree 在高维空间中性能退化问题而设计的空间索引数据结构

核心思想

用一系列层层嵌套的「超球面」来划分数据，利用点到球面的几何距离，在搜索中跳过不可能包含结果的区域

数据结构

二叉树，非叶子节点保存球心和半径，叶子节点保存球心、半径和若干数据

构建过程

Ball-Tree 的每个节点代表一个超球面，包含了该节点下所有数据

根节点的超球面包含了全部数据

叶子节点容量 s：叶子节点的数据量不超过 s

如果节点数据超过 s，要拆成两个不相交的子集，分配到子节点上

从根节点开始向下构建

  1. 为当前节点 N 创建球体

    输入：当前数据集合 G

    计算球心：计算 G 中所有节点的质心（各维度坐标的均值）

    计算半径：计算球心到 G 中所有点的最远距离

  2. 分裂节点

    如果 N 的数据量大于叶子节点容量，需要分裂成两个子集，并希望两个子集尽可能远离，以下是一种常用策略：最远点法

    1. 从 G 中随机选择一个点 p1
    2. 在 G 中找离 p1 最远的点 p2
    3. 将 P 划分到两个集合中：比较 P 中所有点到 p1、p2 的距离，离 p1 更近的点作为左子集PL（包括p1），离 p2 更近的点作为右子集 PR（包括p2）

  3. 递归构建

    1. 使用 PL 递归地构建 N 的左子树
    2. 使用 PR 递归地构建 N 的右子树
    3. 结束条件：当前节点的数据数量小于等于叶子节点容量

搜索过程

先以 K = 1 （最近邻）为例，再推广到 K > 1（KNN）

思路：

  1. 目标点 P，假设当前最近邻节点到 P 距离是 min_dist，如果 P 到超球面的距离 > min_dist，则超球面不会有更近邻的点
  2. 遍历所有节点，利用上述条件，判断是否剪枝
  3. 优先遍历距离更近的节点，得到更小的基准，提高剪枝概率

点 P 到节点 N（超球面球心为 O，半径为 r）的距离： \[ dist(P, N) = max(0, dist(P, O) - r) \] 如果 P 在超球面内，dist(P, N) = 0，如果 P 在超球面外，dist(P, N) > 0

搜索过程如下（从根节点开始，递归进行）：

  1. 使用一个优先队列（最小堆）维护节点的访问顺序（先访问距离近的节点球面），初始最短距离 best_dist = ∞，最近邻点 nearest_neighbor = null
  2. 从根节点开始，将根节点放入优先队列
  3. 从优先队列取出节点
    1. 如果该节点是非叶子节点，检查它的两个子节点：
      1. 对于每个子节点 C，计算 dist(P, C)
      2. 剪枝：如果 dist(P, C) < best_dist，说明该子节点可能存在更近的点，将子节点 C 加入优先队列；否则，跳过整个子树
      3. 如果
    2. 如果该节点是叶子节点，遍历叶子节点内的每个数据点，计算每个点到 P 的距离，如果存在更小距离，更新 best_dist、nearest_neighbor
  4. 终止与返回：当优先队列为空时，此时 nearest_neighbor 即为最近邻

对于 K > 1，只需将 best_dist 和 nearest_neighbor 替换为一个能容纳 K 个候选点的最大堆，best_dist 为堆顶数据点的距离

优缺点

优点：

  1. 高维度搜索性能高：相同数据集，超球面比轴对齐的超平面的几何空间更小，更容易不相交，提高剪枝概率
  2. 对数据分布不敏感：Ball-Tree 不依赖于坐标轴划分，即使某个维度数据分布不均，不会影响平衡
  3. 支持任意距离度量：不仅使用欧式距离，还适用余弦相似度等距离
  4. 结果精确

缺点：

  1. 构建成本高
  2. 内存开销大：每个节点存储球心和半径
  3. 动态更新困难：数据集插入或删除后，重新计算受影响的球心和半径并保持树平衡的成本很高

KD-Tree 与 Ball-Tree 的比较

KD-Tree Ball-Tree
构建速度 更快 较慢
低维数据 更快 较慢
高维数据 差，易退化 远优于 KD-Tree
内存开销 较低 较高
数据分布 敏感 不敏感
距离衡量 仅欧式距离 任意度量
动态更新 成本大 成本大
结果精确 精确 精确

总结

本文介绍了两种精确 KNN 的方法：KD-Tree 和 Ball-Tree，核心思想都是将数据集划分为多个几何空间，通过空间距离进行剪枝，减少遍历数量；

这两种方法有一个共同问题：需要构建一颗静态二叉树，在数据量很大的情况下，构建成本高，数据变化维护难度大，随着二叉树高度增加，检索时间也受影响

有时我们更追求查询时间，不需要完全精确的结果，比如准确率大于 95% 就可以接受，在下一篇文章里将讨论这种近似最近邻的方法