hyperloglog 算法思想与流程

uv (Unique Visitor) ，指在特定时间内访问网站的不同用户数量

本文讨论一种统计 uv 的方法及其原理

问题背景

问题：统计某网站一天的 uv

我的方案：在内存中建立一个 Set，将用户 id 放入 Set 中去重，最后计算 Set 中元素的个数

存在问题：假设一个用户 id 是 36 字节，1亿用户需要3G+空间，如果用户量非常大，内存空间可能不够用

其实我们只关心独立用户的数量，不关心有哪些用户

不保存所有用户能否得到 uv 呢

实现思路

核心思想

首先介绍一种概率思想：

场景：在一次实验中，投10次硬币，每次正反两面的概率相同

问题：首次出现正面在第10次的概率是多少？

答：前9次是反面，第10次是正面的概率是 1/(2¹⁰) = 1/1024 ≈ 0.0009765625，大约需要做 1024 次实验，会出现一次

推广：首次出现正面在第 n 次的概率是 1/(2ⁿ)，平均需要做 2ⁿ次实验可出现一次。可以发现，n 与实验次数是正相关的，通过 n 可以估计出实验次数

回到统计 uv 的问题中，如果把一次访问看作一轮投硬币实验，相同用户的实验结果是固定的，不同用户的实验结果是随机的，统计所有访问的实验结果，每轮计算首次出现正面的次数，记为 n，最后统计 n 的最大值 R，用 R 来估计 uv

用 R 怎么计算 uv 呢？

能否用 uv = 2^R，以 R = 4 为例，从概率模型角度，平均做 16 次实验，会出现一次 R = 4，不过 R = 4 不一定出现在最后一次，有可能第 8 次就出现了 R = 4，但是在第 8 次时我们估计 uv = 16，与实际结果 uv = 8 相差很大

可以用 分桶平均 来减少误差

分桶平均

将数据分为 m 个桶中，每个桶分别估计 uv，再取平均数

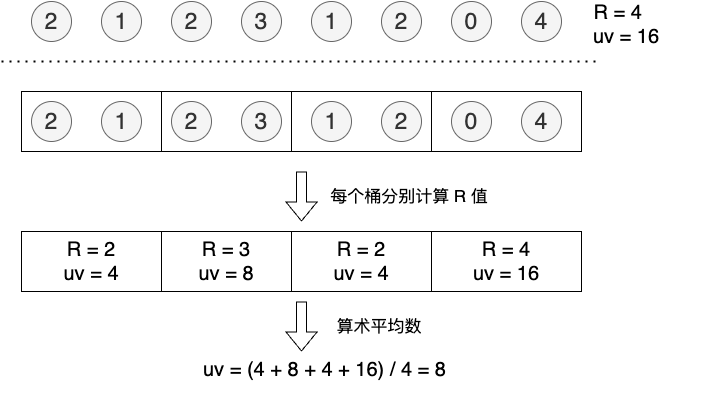
比较单桶、分桶的误差

	结果	误差
单桶	16	100%
分桶	8	0

可以发现，分桶平均后的估计值与实际值更接近，误差更小

调和平均

算术平均数容易受极端值影响，比如某一个桶的 R 极大时，算术平均数会显著高估，使用调和平均数可以加强对离散值的鲁棒性

调和平均数是一组数的倒数的算术平均数的倒数

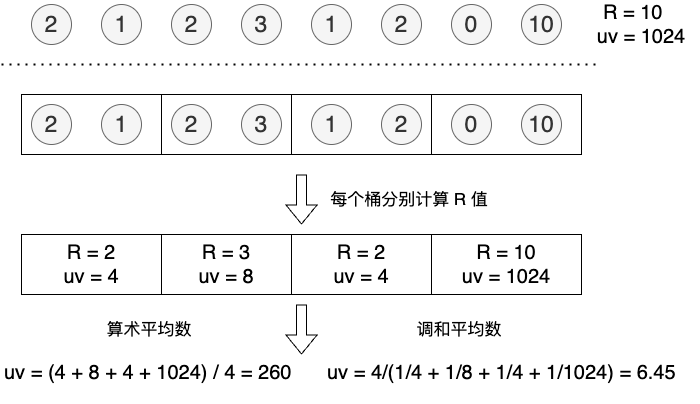
在有极端值时，比较不同计算方式的误差

	结果	误差
单桶	1024	12700%
分桶 - 算术平均数	260	3150%
分桶 - 调和平均数	6.45	19.37%

可以发现，分桶情况下，调和平均数估计结果最接近实际值，误差最小，受极端值影响最少

hyperloglog 就是基于这个思想，来统计大规模数据基数的方法，下面看下具体实现

hyperloglog 执行步骤

步骤1. 哈希映射

目的：将输入元素映射到一个固定长度的二进制串，模拟投硬币实验

方法：使用哈希函数对输入元素求哈希值（固定长度的二进制串），哈希函数具有良好的随机性和均匀性，以确保生成的哈希值尽可能分散

步骤2. 分桶

目的：减少误差

方法：将哈希值分成多个桶，假如哈希值是 64 位，可以将前 6 位作为桶的索引，这样就有 64 个桶

步骤3. 计算前导零

目的：统计每个桶中最大的哈希值前导零数量

方法：对于每个输入元素，计算前导零数量 R（不计算索引部分，即从第 7 位到 64 位），如果 R 大于元素所在桶当前记录的最大 R 值，更新该桶的最大 R 值

步骤4. 计算调和平均数

目的：避免极端数据对平均数的影响过大

方法：计算所有桶中记录的最大前导零数的调和平均数 H \[ H = \frac{m}{\sum_{i=1}^{m}{ {2^{-R[i]}} }} \] 其中，m 是桶的数量，R[i] 是第 i 个桶记录的最大前导零数

步骤5. 基数估算与修正

目的：根据调和平均数估算基数，并进行必要的修正以提高准确性

方法：使用调和平均数来估算基数 E，估算公式为： \[ E = \alpha_m*m*H \] 其中 α_m 是一个与桶数量 m 相关的常数（0.709，m=64时），用于修正估计偏差

对于小基数情况，可能需要额外的修正策略

为什么使用 α_m*m 修正，涉及到比较多的数学问题，目前无法理解

Reference

https://en.wikipedia.org/wiki/HyperLogLog

https://engineering.fb.com/2018/12/13/data-infrastructure/hyperloglog/