数据结构——堆
概念与性质
堆是一个完全二叉树
大根堆：每个子树的最大值都是头节点
小根堆：每个子树的最小值都是头节点
将堆元素按照层次遍历放到一个数组中，则i位置的节点的左孩子位置为2*i+1，右孩子的位置为2*i+2，父节点的位置为(i-1)/2
大根堆
堆中元素用什么存储
很直观的感受，大根堆应该用二叉树来存储数据，不过由于为了维护大根堆的性质，比如需要交换堆顶元素与堆底元素，用二叉树不方便
由于大根堆是满二叉树，每个节点与其父节点、孩子节点在数组下标上有规律可循（见上文），故用数组存储堆中元素
堆大小
既然堆中元素用数组存储，由于数组长度在申请内存空间时即设定，需要用一个单独的变量（heapSize）记录堆中元素的个数，如数组长度为100，heapSize=20
堆的基本操作
节点上升
对于任意节点，如果大于父节点（通过访问(i-1)/2位置找到父节点），与父节点交互，再与新的父节点比较，直到小于父节点或到达根节点
1
2
3
4
5
6
| private static void siftUp(int[] arr, int index) {
while (arr[index] > arr[(index - 1) / 2]) {
swap(arr, index, (index - 1) / 2);
index = (index - 1) / 2;
}
}
|
节点下沉
对于任意节点，如果小于较大的子节点，交换，直到不小于较大子节点或到达叶子节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| private static void siftDown(int[] arr, int index, int heapSize) {
int leftChildIndex = index * 2 + 1;
while (leftChildIndex <heapSize) {
int largest = leftChildIndex + 1 < heapSize && arr[leftChildIndex + 1] > arr[leftChildIndex] ?
leftChildIndex + 1 : leftChildIndex;
largest = arr[largest] > arr[index] ? largest : index;
if (largest == index) {
break;
}
swap(arr, index, largest);
index = largest;
leftChildIndex = index * 2 + 1;
}
}
|
向堆中插入元素
将堆大小加一，插入的元素放在数组末尾（堆尾），再将堆尾节点上升
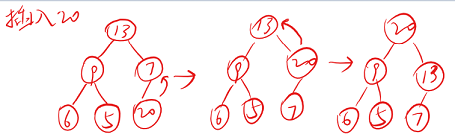image-20220604152134239
1
2
3
4
5
6
7
8
9
10
11
| public boolean add(int n) {
if (this.size >= arr.length) {
this.grow();
}
this.size ++;
this.arr[this.size-1] = n;
siftUp(this.arr, this.size-1);
return true;
}
|
弹出最大值
将数组0位置元素（堆顶）与最后位置元素（堆尾）交互，有效长度减一，再将堆顶元素下沉
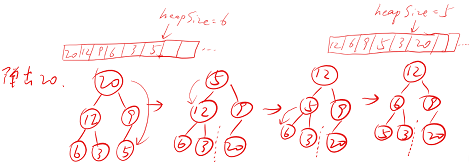image-20220604161702736
1
2
3
4
5
6
7
8
9
10
11
| public int poll() {
if (this.isEmpty()) {
throw new RuntimeException("堆已空，无法弹出元素");
}
int root = this.arr[0];
swap(this.arr, 0, this.size-1);
this.size --;
this.siftDown(this.arr, 0, this.size);
return root;
}
|
堆排序
问题描述：给定一个无序数组，将其升序排列
思路：
- 将无序数组构造为大顶堆
- 将堆顶（最大值）弹出（与数组末尾元素交互，堆大小减一，新堆顶下沉）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| public static void sort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int i = arr.length - 1; i >= 0; i--) {
siftDown(arr, i, arr.length);
}
int heapSize = arr.length;
while (heapSize > 0) {
swap(arr, 0, --heapSize);
siftDown(arr, 0, heapSize);
}
}
|
思考：将无序数组构造大顶堆有几种方式，哪种最快
| 自上而下，依次上升 |
正确 |
对于一个节点，最坏情况：从叶子节点上升至根节点 |
| 自下而上，依次上升 |
错误 |
- |
| 自上而下，依次下沉 |
错误 |
- |
| 自下而上，依次下沉 |
正确 |
对于一个节点，最坏情况：从根节点下沉到叶子节点 |
直观感受：由于满二叉树中，叶子节点个数为N/2，非叶子节点个数为N/2，上升或下沉的时间复杂度与路径长度有关，最长为logN，如果自上而下，依次上升，导致大部分节点要上升的路径很长；如果自下而上，依次下沉，叶子节点不需要变动，大部分节点下沉的路径很短
时间复杂度分析：待补充
故采用自下而上，依次下沉的方式来将数组构造为大顶堆
大根堆的完整代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
| import java.util.Arrays;
public class Heap {
private final static Integer DEFAULT_INITIAL_CAPACITY = 11;
private int[] arr;
public Heap() {
this(DEFAULT_INITIAL_CAPACITY);
}
public Heap(int initialCapacity) {
if (initialCapacity < 1) {
throw new IllegalArgumentException();
}
this.arr = new int[DEFAULT_INITIAL_CAPACITY];
}
private int size;
public int getSize() {
return this.size;
}
private void grow() {
int oldCapacity = arr.length;
this.arr = Arrays.copyOf(this.arr, oldCapacity * 2);
}
public boolean add(int n) {
if (this.size >= arr.length) {
this.grow();
}
this.arr[this.size] = n;
siftUp(this.arr, this.size);
this.size ++;
return true;
}
public int peek() {
return arr[0];
}
public int poll() {
if (this.isEmpty()) {
throw new RuntimeException("堆已空，无法弹出元素");
}
int root = this.arr[0];
swap(this.arr, 0, this.size-1);
this.size --;
this.siftDown(this.arr, 0, this.size);
return root;
}
public static void sort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int i = arr.length - 1; i >= 0; i--) {
siftDown(arr, i, arr.length);
}
int heapSize = arr.length;
while (heapSize > 0) {
swap(arr, 0, --heapSize);
siftDown(arr, 0, heapSize);
}
}
private static void siftUp(int[] arr, int index) {
while (arr[index] > arr[(index - 1) / 2]) {
swap(arr, index, (index - 1) / 2);
index = (index - 1) / 2;
}
}
private static void siftDown(int[] arr, int index, int heapSize) {
int leftChildIndex = index * 2 + 1;
while (leftChildIndex <heapSize) {
int largest = leftChildIndex + 1 < heapSize && arr[leftChildIndex + 1] > arr[leftChildIndex] ?
leftChildIndex + 1 : leftChildIndex;
largest = arr[largest] > arr[index] ? largest : index;
if (largest == index) {
break;
}
swap(arr, index, largest);
index = largest;
leftChildIndex = index * 2 + 1;
}
}
public boolean isEmpty() {
return this.size == 0;
}
@Override
public String toString() {
return "Heap{" +
"arr=" + Arrays.toString(arr) +
", size=" + size +
'}';
}
private static void swap(int[] arr, int i, int j) {
int t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
}
|
代码中存在的问题：
- 只支持单一类型
- 数组扩容方式暴力，存在OOM隐患
- 堆排序只支持升序
思考：
- 如何合理的让堆的数据动态扩容
JDK中PriorityQueue代码解读
Object[] queue 的动态扩容方法
由于每次扩容都需要拷贝整个数组，故需要控制扩容的次数不要太频繁；如果每次扩容量太大，可以减少扩容频率，但存在空间的浪费
如何找到二者的平衡呢，下面是JDK的实现方案
设置最小扩容量minCapacity，每次需要扩容时，扩容到原size的1.5倍，如果这个扩容量没有达到minCapacity，则直接扩容到minCapacity
1
2
3
4
5
6
7
8
9
| private void grow(int minCapacity) {
int oldCapacity = queue.length;
int newCapacity = ArraysSupport.newLength(oldCapacity,
minCapacity - oldCapacity,
oldCapacity < 64 ? oldCapacity + 2 : oldCapacity >> 1
);
queue = Arrays.copyOf(queue, newCapacity);
}
|
为什么 Object[] queue
前要加 transient
transient 令属性不再可序列化和反序列化
transient 的使用场景：一些不应该设为 static
的属性，不进行序列化（静态属性不会被序列化），如 Logger
实例，安全性的信息
transient 的原因：由于 Object[] queue
的长度是动态扩容产生的，即根据heapSize，设定合理的queue长度，故queue中存在很多没有存储实际数据的空间，将
queue 整体直接序列化，可能存在空间浪费。通过 writeObject 序列化，可通过
heapSize 自行控制，只序列化实际存储数据部分的queue；而利用 readObject
反序列化时，先获取
heapSize，再初始化queue中的值，并根据heapSize，动态设定合理的容量